Kvarc órák NAPI járáseltérése | DAILY deviation of quartz watches

Noha a kvarc órák alacsonyabb járáseltérése miatt pontosságukat általában a havi méréssel ellenörzöm, néhány különleges kvarcórát napi méréssel is ellenörzöm. Elsösorban korai kvarcórákat, nelyek napi járáseltérése még közel van a mechanikus órákhoz, illetve a Seiko kvarc-mechanikus hibrid óráját soroltam ide.
 Although due to the lower deviation of the quartz watches monthly measurement is taken, I measure some special quartz watches on daily basis. First of all the early quartz watches. Their daily deviation is similar to the mechanical watches. I have put in this category the quartz-mechanical hybrid waych of Seiko as well.
No. __ Watch Daily avg. Daily st. Dev. Days Prod. Caliber  

1  

  Grand Seiko Spring Drive - test2

0.27  

0.4472  

244  

2006  

 9R65  

 

2  

  Grand Seiko Spring Drive

0.28  

0.4504  

730  

2006  

 9R65  

(x)

3  

  Omega f=8192

2.66  

0.4755  

445  

1970  

 1301  

(x)

4  

  Seiko AGS

-1.52  

2.9729  

100  

1988  

 AGS  

(x)
         

1519  

     
No. __ Óra Napi átlag Napi szórás Napok Gyártva Szerkezet  
  • A kaliber nevére kattintva annak ismertetéséhez jut.
  • Napi hordás közbeni teszt
  • (x) a méréssorozat befejezödött.
  • By clicking on the name of the caliber you will see the description of it.
  • Live daily wear Test.
  • (x) test was finished.

    Szimuláció: kvarc órák NAPI járáseltérése | Simulation: DAILY deviation of quartz watches

Mivel tapasztlat szerint a kvarcórák eltérése napról-napra nem "ugrál", bizonyos feltételek mellett szimulálhatjuk a napi eltérések szórását is.
  • A feltétel az, hogy az óra havi járáseltérése ne haladja meg a 28 másodpercet.
  • A módszer az, hogy a havi eltérés másodperceit elosztjuk a hónap napjai között, úgy, hogy egy nap eltérése 0, vagy 1 mp legyen.
  • Az ereményül kapott táblát ugyanúgy értékeljük ki, mint a napi mérésekéit.
Az eredméneyek itt láthatóak:

Since the experience shows that the devation of quartz watches do not oscillate under certain condition we can simulate the standard deviation of the daily deviations.
  • The condition is that the monthly deviation of the watch should not axceed 28 seconds.
  • The method is that the seconds of the monthly deviation are distributed among the days of the month the was the daily deviation can only be 0 or 1 sec.
  • The resulting table is evaluated the same way as of the daily recordings.
You can see the results here:

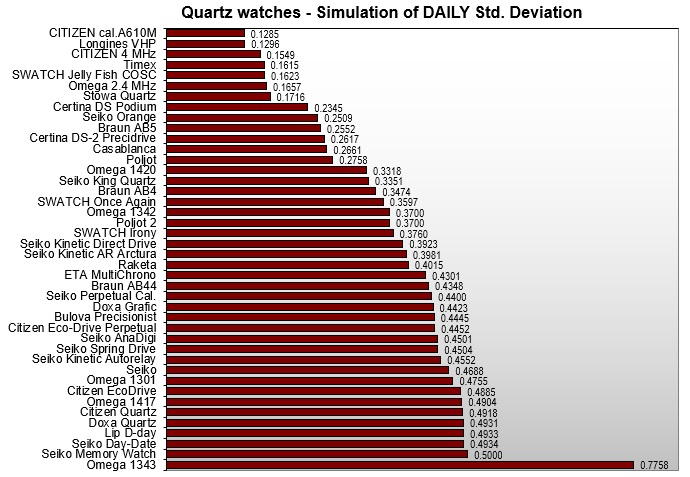
No. __ Watch Daily avg. Daily st.dev. Days  

1  

  Longines VHP

0.02  

0.1296  

6498  

QC

2  

  CITIZEN cal.A610M

0.02  

0.1318  

5326  

QC

3  

  CITIZEN 4 MHz

0.02  

0.1549  

577  

[QC]

4  

  Timex

0.02  

0.1615  

3164  

(x)

5  

  SWATCH Jelly Fish COSC

0.02  

0.1623  

2646  

[QC]

6  

  Omega 2.4 MHz

0.02  

0.1657  

790  

[QC]

7  

  Stowa Quartz

0.03  

0.1716  

396  

(x)

8  

  Certina DS Podium

0.06  

0.2311  

3986  

9  

  Seiko Orange

0.07  

0.2509  

2573  

(x)

10  

  Braun AB5

0.07  

0.2552  

972  

(x)

11  

  Certina DS-2 Precidrive

0.07  

0.2575  

1919  

12  

  Casablanca

-0.08  

0.2661  

731  

(x)

13  

  Poljot

0.02  

0.2758  

761  

(x)

14  

  Omega 1420

-0.13  

0.3318  

1216  

(x)

15  

  Seiko King Quartz

0.01  

0.3351  

366  

(x)

16  

  Braun AB4

0.14  

0.3474  

792  

(x)

17  

  SWATCH Once Again

0.12  

0.3597  

427  

(x)

18  

  Omega 1342

1.10  

0.3700  

455  

(x)

19  

  Poljot 2

0.16  

0.3700  

1644  

(x)

20  

  SWATCH Irony

0.17  

0.3760  

1157  

(x)

21  

  Seiko Kinetic Direct Drive

0.19  

0.3923  

4660  

22  

  Seiko Kinetic AR Arctura

0.20  

0.3981  

1492  

(x)

23  

  Raketa

0.20  

0.4015  

1219  

(x)

24  

  ETA MultiChrono

0.24  

0.4301  

944  

(x)

25  

  Braun AB44

0.25  

0.4348  

669  

(x)

26  

  Seiko Perpetual Cal.

0.26  

0.4400  

5140  

27  

  Doxa Grafic

0.27  

0.4414  

6557  

28  

  Seiko AnaDigi

0.28  

0.4501  

884  

(x)

29  

  Seiko Spring Drive

0.28  

0.4504  

730  

(D)

30  

  Bulova Precisionist

0.28  

0.4510  

4200  

31  

  Citizen Eco-Drive Perpetual

0.27  

0.4510  

4081  

32  

  Seiko Kinetic Autorelay

0.29  

0.4552  

2312  

(x)

33  

  Seiko

0.33  

0.4688  

6141  

34  

  Omega 1301

2.66  

0.4755  

445  

(D)

35  

  Citizen EcoDrive

0.39  

0.4885  

2071  

(D)

36  

  Omega 1417

0.60  

0.4904  

1248  

(x)

37  

  Citizen Quartz

0.41  

0.4918  

518  

(x)

38  

  Doxa Quartz

0.58  

0.4931  

643  

(x)

39  

  Lip D-day

0.42  

0.4933  

642  

(x)

40  

  Seiko Day-Date

0.58  

0.4934  

579  

(x)

41  

  Seiko Memory Watch

0.52  

0.5000  

883  

(x)

42  

  Omega 1343

-0.46  

0.7758  

517  

(x)
       

82971 

    
No. __ Óra Napi átlag Napi szórás Napok  
  • Az óra nevére kattintva annak mérési eredményeit láthatja.
  • QC Teljesíti a kvarc kronométer követelményeit.
  • (D) Valóban napi mérés történt.
  • (x) a méréssorozat befejezödött.
  • By clicking on the name of the watch you will see the test results.
  • QC Meets the criteria of quartz cronometer.
  • (D) Daily test was carried out.
  • (x) test was finished.

    A konverzió módszere és hibája | Method of conversion and its error

Az alábbi ábrán a vízszintes tengelyen egy hónap napjai láthatóak.
A függöleges tengelyen az átszámított értékek vannak.
A ferde vonal a lineáris konverziót mutatja. A Pontok a lépcsözetes elosztási módszert mutatja.
 On the chart below on the horizontal axis are the days of a month.
On the vertical axis the converted daily deviation values.
The line represents the linear method of distribution. The points show the step-by-step method.
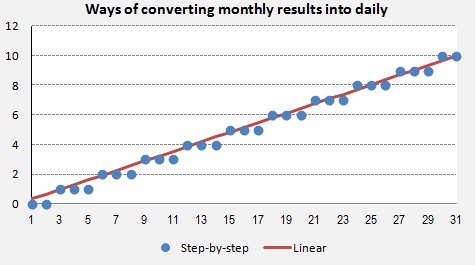
Vizsgáljuk meg, hogy mekkora hibát követünk el a lépcsös elosztással.

31 esetre kiszámítottam a két módszeböl adódó szórást.

Az alábbi ábrán a vízszintes tengelyen a vizsgált esetek havi eltérései láthatóak.
A függöleges tengelyen az átszámított értékekböl számított szórások vannak.
A ferde vonal a lineáris konverziót mutatja. A Pontok a lépcsözetes elosztási módszert mutatja.
A plusz jelekkel rajzolt görbe az elözö két görbe különbsége azaz a módszerek különbsége. 		Let us see how large error we commit by using step-by-step method.

I have calculated for 31 cases the standard deviations resulting from the two methods.

On the chart below on the horizontal axis are the monthly deviations of the tested cases.
On the vertical axis are the standard deviation values calculated from the converted values.
The slant line shows the linear method. Points represent the step-by-step conversion method.
The curve displayed by plus signs shows the difference of the two curves thus the two methods.
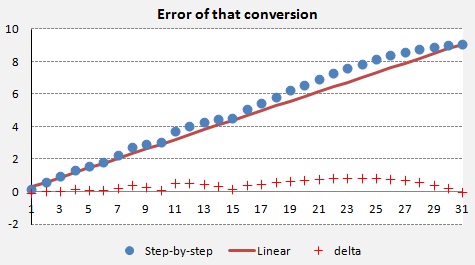
Miért nem a lineáris módszer? Why not to use linear method?
  • A mechanikus órák leolvasása is napi.
  • Ott is csak kerek másodpercnyi eltéréseket veszek figyelembe.
  • A két módszer eltérése kicsi.
  • A havi 1 mp eltérés estét leszámítva a lépcsös módszer magasabb értéket ad.
  • Tehát a kvarc chronometereket leszámítva kicsit rosszabbnak mutatja a kvarcórákat.
  • Read-out of the mechanical watches is done daily.
  • I accept only full second daily deltas.
  • Difference of the two methods is small.
  • Except the monthly 1 sec deviation the step-by-step method gives higher values.
  • Thus except the quartz chronometers that method shows the quartz watches worse than they are.

www.mechanikus.hu